18.1. Skip Lists¶

This section presents a probabilistic search structure called the Skip List. Like the BST, Skip Lists are designed to overcome a basic limitation of array-based and linked lists: Either search or update operations require linear time. The Skip List is an example of a probabilistic data structure, because it makes some of its decisions at random.

Skip Lists provide an alternative to the BST and related tree structures. The primary problem with the BST is that it may easily become unbalanced. The 2-3 Tree is guaranteed to remain balanced regardless of the order in which data values are inserted, but it is rather complicated to implement. The AVL tree and the splay tree are also guaranteed to provide good performance, but at the cost of added complexity as compared to the BST. The Skip List is easier to implement than known balanced tree structures. The Skip List is not guaranteed to provide good performance (where good performance is defined as \(\Theta(\log n)\) search, insertion, and deletion time), but it will provide good performance with extremely high probability (unlike the BST which has a good chance of performing poorly). As such it represents a good compromise between difficulty of implementation and performance.

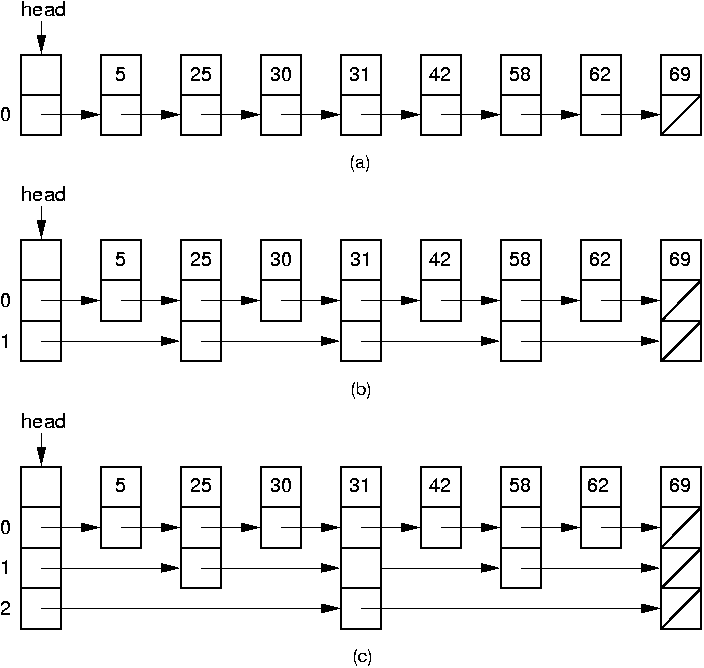
Figure 18.1.1: Illustration of the Skip List concept. (a) A simple linked list. (b) Augmenting the linked list with additional pointers at every other node. To find the node with key value 62, we visit the nodes with values 25, 31, 58, and 69, then we move from the node with key value 58 to the one with value 62. (c) The ideal Skip List, guaranteeing \(O(\log n)\) search time. To find the node with key value 62, we visit nodes in the order 31, 69, 58, then 69 again, and finally, 62.

Figure 18.1.1 illustrates the concept behind the Skip List. Part (a) shows a simple linked list whose nodes are ordered by key value. To search a sorted linked list requires that we move down the list one node at a time, visiting \(\Theta(n)\) nodes in the average case. What if we add a pointer to every other node that lets us skip alternating nodes, as shown in part (b)? Define nodes with a single pointer as level 0 Skip List nodes, and nodes with two pointers as level 1 Skip List nodes.

To search, follow the level 1 pointers until a value greater than the search key has been found, go back to the previous level 1 node, then revert to a level 0 pointer to travel one more node if necessary. This effectively cuts the work in half. We can continue adding pointers to selected nodes in this way --- give a third pointer to every fourth node, give a fourth pointer to every eighth node, and so on—until we reach the ultimate of \(\log n\) pointers in the first and middle nodes for a list of \(n\) nodes as illustrated in Figure 18.1.1 Part (c). To search, start with the bottom row of pointers, going as far as possible and skipping many nodes at a time. Then, shift up to shorter and shorter steps as required. With this arrangement, the worst-case number of accesses is \(\Theta(\log n)\).

We will store with each Skip List node an array named forward that stores the pointers as shown in Figure 18.1.1 Part (c). Position forward[0] stores a level 0 pointer, forward[1] stores a level 1 pointer, and so on. The Skip List object includes data member level that stores the highest level for any node currently in the Skip List. The Skip List stores a header node named head with level pointers. The find function is shown next.

// Return the (first) matching matching element if one exists, null otherwise
public KVPair<K,E> search(Comparable<K> key) {
  boolean found = false;
  SkipNode x = head;                     // Dummy header node
  for (int i=level; i>=0; i--)           // For each level...
    while ((x.forward[i] != null) &&
           (key.compareTo(x.forward[i].element().key()) > 0)) // go forward
      x = x.forward[i];              // Go one last step
  x = x.forward[0];  // Move to actual record, if it exists
  if ((x != null) && (key.compareTo(x.element().key()) == 0))
    return x.element();
  else
    return null;
}

Searching for a node with value 62 in the Skip List of Figure 18.1.1 Part (c) begins at the header node. Follow the header node's pointer at level, which in this example is level 2. This points to the node with value 31. Because 31 is less than 62, we next try the pointer from forward[2] of 31's node to reach 69. Because 69 is greater than 62, we cannot go forward but must instead decrement the current level counter to 1. We next try to follow forward[1] of 31 to reach the node with value 58. Because 58 is smaller than 62, we follow 58's forward[1] pointer to 69. Because 69 is too big, follow 58's level 0 pointer to 62. Because 62 is not less than 62, we fall out of the while loop and move one step forward to the node with value 62.

The ideal Skip List of Figure 18.1.1 Part (c) has been organized so that (if the first and last nodes are not counted) half of the nodes have only one pointer, one quarter have two, one eighth have three, and so on. The distances are equally spaced; in effect this is a "perfectly balanced" Skip List. Maintaining such balance would be expensive during the normal process of insertions and deletions. The key to Skip Lists is that we do not worry about any of this. Whenever inserting a node, we assign it a level (i.e., some number of pointers). The assignment is random, using a geometric distribution yielding a 50% probability that the node will have one pointer, a 25% probability that it will have two, and so on. The following function determines the level based on such a distribution:

/** Pick a level using a geometric distribution */
int randomLevel() {
  int lev;
  for (lev=0; DSutil.random(2) == 0; lev++); // Do nothing
  return lev;
}

Once the proper level for the node has been determined, the next step is to find where the node should be inserted and link it in as appropriate at all of its levels. Here is an implementation for inserting a new value into the Skip List.

/** Insert a KVPair into the skiplist */
public boolean insert(KVPair<K,E> it) {
  int newLevel = randomLevel();
  Comparable<K> k = it.key();
  if (level < newLevel)
    adjustHead(newLevel);
  @SuppressWarnings("unchecked") // Generic array allocation
  SkipNode[] update = (SkipNode[])Array.newInstance(SkipList.SkipNode.class, level+1);
  SkipNode x = head;        // Start at header node
  for (int i=level; i>=0; i--) { // Find insert position
    while((x.forward[i] != null) && (k.compareTo((x.forward[i]).element().key()) > 0))
      x = x.forward[i];
    update[i] = x;               // Track end at level i
  }	
  x = new SkipNode(it, newLevel);
  for (int i=0; i<=newLevel; i++) {      // Splice into list
    x.forward[i] = update[i].forward[i]; // Who x points to
    update[i].forward[i] = x;            // Who y points to
  }
  size++;                       // Increment dictionary size
  return true;
}

Figure 18.1.2 illustrates the Skip List insertion process. In this example, we begin by inserting a node with value 10 into an empty Skip List. Assume that randomLevel returns a value of 1 (i.e., the node is at level 1, with 2 pointers). Because the empty Skip List has no nodes, the level of the list (and thus the level of the header node) must be set to 1. The new node is inserted, yielding the Skip List of Figure 18.1.2 part (a).

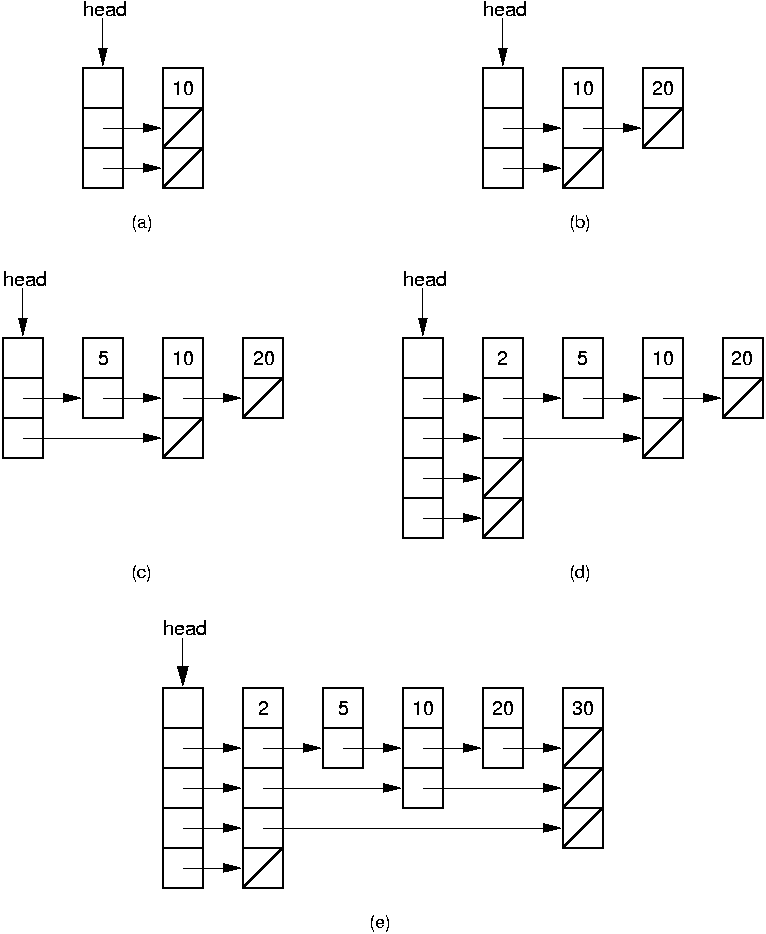
Figure 18.1.2: Illustration of Skip List insertion. (a) The Skip List after inserting initial value~10 at level 1. (b) The Skip List after inserting value 20 at level 0. (c) The Skip List after inserting value 5 at level 0. (d) The Skip List after inserting value 2 at level 3. (e) The final Skip List after inserting value 30 at level 2.

Next, insert the value 20. Assume this time that randomLevel returns 0. The search process goes to the node with value 10, and the new node is inserted after, as shown in Figure 18.1.2 part (b). The third node inserted has value 5, and again assume that randomLevel returns 0. This yields the Skip List of Figure 18.1.2 part (c).

The fourth node inserted has value 2, and assume that randomLevel returns 3. This means that the level of the Skip List must rise, causing the header node to gain an additional two (null) pointers. At this point, the new node is added to the front of the list, as shown in Figure 18.1.2 part (d).

Finally, insert a node with value 30 at level 2. This time, let us take a close look at what array update is used for. It stores the farthest node reached at each level during the search for the proper location of the new node. The search process begins in the header node at level 3 and proceeds to the node storing value 2. Because forward[3] for this node is null, we cannot go further at this level. Thus, update[3] stores a pointer to the node with value 2. Likewise, we cannot proceed at level 2, so update[2] also stores a pointer to the node with value 2. At level 1, we proceed to the node storing value 10. This is as far as we can go at level 1, so update[1] stores a pointer to the node with value 10. Finally, at level 0 we end up at the node with value 20. At this point, we can add in the new node with value 30. For each value i, the new node's forward[i] pointer is set to be update[i]->forward[i], and the nodes stored in update[i] for indices 0 through 2 have their forward[i] pointers changed to point to the new node. This "splices" the new node into the Skip List at all levels.

The remove function is left as an exercise. It is similar to insertion in that the update array is built as part of searching for the record to be deleted. Then those nodes specified by the update array have their forward pointers adjusted to point around the node being deleted.

A newly inserted node could have a high level generated by randomLevel, or a low level. It is possible that many nodes in the Skip List could have many pointers, leading to unnecessary insert cost and yielding poor (i.e., \(\Theta(n)\) performance during search, because not many nodes will be skipped. Conversely, too many nodes could have a low level. In the worst case, all nodes could be at level 0, equivalent to a regular linked list. If so, search will again require \(\Theta(n)\) time. However, the probability that performance will be poor is quite low. There is only one chance in 1024 that ten nodes in a row will be at level 0. The motto of probabilistic data structures such as the Skip List is "Don't worry, be happy". We simply accept the results of randomLevel and expect that probability will eventually work in our favor. The advantage of this approach is that the algorithms are simple, while requiring only \(\Theta(\log n)\) time for all operations in the average case.

In practice, the Skip List will probably have better performance than a BST. The BST can have bad performance caused by the order in which data are inserted. For example, if \(n\) nodes are inserted into a BST in ascending order of their key value, then the BST will look like a linked list with the deepest node at depth \(n-1\). The Skip List's performance does not depend on the order in which values are inserted into the list. As the number of nodes in the Skip List increases, the probability of encountering the worst case decreases geometrically. Thus, the Skip List illustrates a tension between the theoretical worst case (in this case, \(\Theta(n)\) for a Skip List operation), and a rapidly increasing probability of average-case performance of \(\Theta(\log n)\), that characterizes probabilistic data structures.