287. Recursively Enumerable Languages¶

287.1. Recursively Enumerable Languages¶

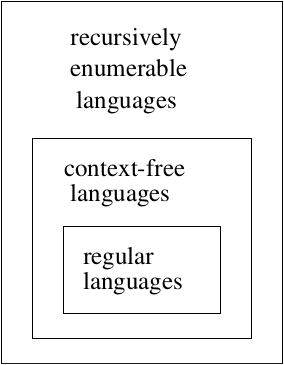
What is the set of languages that TM’s accept? We know that they accept RL’s and CFL’s. And additional languages.

Question: Is there any language that a TM cannot accept?

Definition: A language $L$ is recursively enumerable if there exists a TM $M$ such that $L = L(M)$ .

[Hah! All that says is that the languages that a TM can deal with now have a name!]

We say that $M$ accepts the language. For every $w$ in $L$ , $M$ should accept $w$ .

Question: What happens if $w$ is not in $L$ ? Saying that $M$ can properly accepting strings in $L$ doesn’t define happens if $w$ is not in $L$ . $M$ may not halt in that case.

Note: We do not get a yes or no answer, just a yes if w is in L!

Definition: A language $L$ is recursive if there exists a TM $M$ such that $L = L(M)$ and $M$ halts on every $w \in \Sigma^+$ . Thus, A language $L$ is recursive if and only if there exists a membership algorithm for it.

[Note the difference beteen a recursive language (one that is recognized by a TM) and a recursive algorithm (which merely means that it calls itself).]

NOTE: We will ignore the empty string. In Chapter 9, the definition of the TM assumes that the input string is always padded on both sides of the input. If the input could be a blank, the tape head would not know where the input string was. It would be easy to adjust the definition to include the empty string, but for now we will just examine languages that do not include $\lambda$ .

Note

Not a problem if we use a one-sided tape as our base definition, which is a good argument for doing it that way.

287.1.1. Enumeration procedure for recursive languages¶

To enumerate all $w \in \Sigma^+$ in a recursive language $L$ :

* Let

$M$ be a TM that recognizes

$L, L = L(M)$ .

* Construct 2-tape TM

$M'$

Tape 1 will enumerate the strings in

$\Sigma^+$

Tape 2 will enumerate the strings in

$L$ .

- On Tape 1 generate the next string

$v$ in

$\Sigma^+$

- Simulate

$M$ on

$v$

$M$ accepts

$v$ , then write

$v$ on Tape 2.

287.1.2. Enumeration procedure for recursively enumerable languages¶

The above procedure does not work, since $M$ might not halt on strings that are not in the language.

To enumerate all $w \in \Sigma^+$ in a recursively enumerable language $L$ :

Repeat forever:

* Generate next string (Suppose k strings have been generated:

$w_1, w_2, ..., w_k$ )

* Run

$M$ for one step on

$w_k$ .

Run M for two steps on wk−1.
…
Run M for k steps on w1.
If any of the strings are accepted then write them to Tape 2.
NOTE: Accepted in the exact number of steps!

$\begin{split}\begin{array}{llll} 1\ \mbox{move} \ w_1 \\ 1\ \mbox{move} \ w_2 & 2\ \mbox{moves} \ w_1 \\ 1\ \mbox{move} \ w_3 & 2\ \mbox{moves} \ w_2 & 3\ \mbox{moves} \ w_1 \\ 1\ \mbox{move} \ w_4 & 2\ \mbox{moves} \ w_3 & 3\ \mbox{moves} \ w_2 & 4\ \mbox{moves}\ w_1 \\ ... \\ \end{array}\end{split}$

Questions:

Are there languages that are RE but not recursive? yes.
Are there languages that are not RE? yes

We will prove that there is a language that is not recursively enumerable.

Note

Ask what is a powerset. $2^{\{a,b\}}, 2^{pos. int.}$

Theorem 1

Theorem: Let $S$ be an infinite countable set. Its powerset $2^S$ is not countable.

Proof: Use diagonalization

S is countable, so its elements can be enumerated.
S={s1,s2,s3,s4,s5,s6…}
An element t∈2S can be represented by a sequence of
0’s and 1’s such that the i th position in t is 1
if si is in t, 0 if si is not in t.
Example, {s2,s3,s5} represented by 0110100…
Example, set containing every other element from S,
starting with s1 is {s1,s3,s5,s7,…}
represented by 101010101010…
Suppose 2S is countable.
Then we can emunerate all its elements: t1,t2,...
HEADINGS S on columns 2S on rows

$\begin{split}\begin{array}{c|cccccccc} & s_1 & s_2 & s_3 & s_4 & s_5 & s_6 & s_7 & ... \\ \hline t_1 & \underline{0} & 1 & 0 & 1 & 0 & 0 & 1 & ... \\ t_2 & 1 & \underline{1} & 0 & 0 & 1 & 1 & 0 & ... \\ t_3 & 0 & 0 & \underline{0} & 0 & 1 & 0 & 0 & ... \\ t_4 & 1 & 0 & 1 & \underline{0} & 1 & 1 & 0 & ... \\ t_5 & 1 & 1 & 1 & 1 & \underline{1} & 1 & 1 & ... \\ t_6 & 1 & 0 & 0 & 1 & 0 & \underline{0} & 1 & ... \\ t_7 & 0 & 1 & 0 & 1 & 0 & 0 & \underline{0} & ... \\ ... & \\ \\ \hline \hline \hat{t} & 1 & 0 & 1 & 1 & 0 & 1 & 1 & ...\\ \end{array}\end{split}$

NOTE:

$i$ th position in

$\hat{t} = 0$ if

$s_i = 1$ , 1 if

$s_i = 0$ .

Construct an element

$\hat{t}$ such that the

$i$ th position in

$\hat{t}$ equals 0 if the

$i$ th position in

$t_i$ is 1, and equals 1 if the

$i$ th position in

$t_i$ is 0.

Notice that

$\hat{t} \neq t_i$ for any

$i$ . Yet

$\hat{t}$ represents an element from

$2^S$ . Contradiction!

$2^S$ is not a countable set. QED.

Theorem 2

Theorem: For any nonempty $\Sigma$ , there exist languages that are not recursively enumerable.

Proof:

A language is a subset of Σ∗.
The set of all languages over Σ is
2Σ∗.
⇒ the set of all languages over Σ
is not countable.
The set of all TM’s is countable.
Thus, set of recursively enumerable languages are countable.
⇒ there are languages that are not recursively
enumerable. QED.

Theorem 3

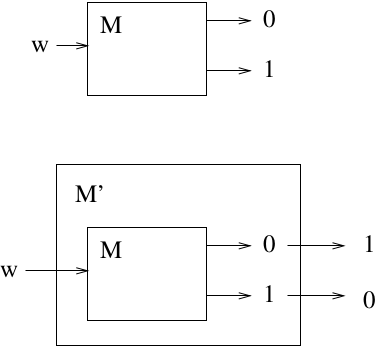
Theorem: There exists a recursively enumerable language $L$ such that $\bar L$ is not recursively enumerable.

Proof:

Let Σ={a}
Enumerate all TM’s over Σ: M1,M2,M3,...
For each TM Mi, L(Mi) is a RE (recursively
enumerable) language.
For each RE language, there is a TM that accepts it.
Construct a new L={ai|ai∈L(Mi)}.
L is a RE language.
Can come up with an algorithm to list out all of its elements.
Enumerate the TM codes until you generate the code for TM Mi.
Generate the string ai.
Using the universal TM, simulate Mi on ai.
If ai is in L(Mi) then the simulation will halt.

$\begin{split}\begin{array}{c|cccccc} & a & aa & aaa& aaaa& aaaaa& ... \\ \hline L(M_1) & 0 & 1 & 1 & 0 & 1 & ... \\ L(M_2) & 1 & 0 & 1 & 0 & 1 & ... \\ L(M_3) & 0 & 0 & 1 & 1 & 0 & ... \\ L(M_4) & 1 & 1 & 0 & 1 & 1 & ... \\ L(M_5) & 0 & 0 & 0 & 1 & 0 & ... \\ ... & \\ \\ \hline \hline L & 0 & 0 & 1 & 1 & 0 & ... \\ \bar{L}& 1 & 1 & 0 & 0 & 1 & ... \\ \end{array}\end{split}$

Let ˉL={ai|ai∉L(Mi)}
Enumerate all the RE languages and identify which strings are in
each language.
A ‘0’ entry means no the string is not in the language,
and a ‘1’ entry means yes, the string is in the language.
ˉL is not a RE language!
ˉL cannot equal any of the RE languages
that are enumerated above because it differs in the i th
position. QED
NOTE: You cannot come up with an algorithm to list out its
elements.
The above algorithm for listing L ‘s elements does not
work to list ˉL ‘s elements.

The next two theorems in conjunction with the previous theorem will show that there are some languages that are recursively enumerable, but not recursive.

Theorem 4

Theorem: If languages $L$ and $\bar{L}$ are both RE, then L is recursive.

Proof:

There exists M1 such that M1 can enumerate all
elements in L.
There exists M2 such that M2 can enumerate all
elements in ˉL.
To determine if a string w is in L or not in
L, perform the following algorithm:

Repeat until w matched
Enumerate next element in M1
Enumerate next element in M2

If w is enumerated from M1, then w is in
L.
If w is enumerated from M2, then w is not
in L.
For each w∈Σ∗ we can determine if w is
in L or not in L.
Thus, L is recursive. QED.

Theorem 5

Theorem: If $L$ is recursive, then $\bar{L}$ is recursive.

Proof:

$L$ is recursive, so there exists a TM

$M$ such that

$M$ can determine if

$w$ is in

$L$ or

$w$ is not in

$L$ .

$M$ outputs a 1 if a string

$w$ is in

$L$ , and outputs a 0 if a string

$w$ is not in

$L$ .

Construct TM

$M'$ that does the following.

$M'$ first simulates TM

$M$ . If TM

$M$ halts with a 1, then

$M'$ erases the 1 and writes a 0. If TM

$M$ halts with a 0, then

$M'$ erases the 0 and writes a 1.

$M'$ can determine if a string

$w$ is in

$\bar{L}$ or not in

$\bar{L}$ .

Thus,

$\bar{L}$ is recursive. QED.

If $L$ is not recursive, then neither $L$ nor $\bar{L}$ can be RE.

The language $L = \{ a^i | a^i \in L(M_i) \}$ is RE but not recursive (since we proved that its complement was not RE).

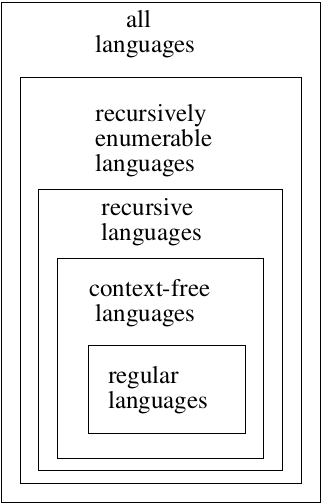
Hierarchy of Languages:

Now we will look at the grammar that represents the same language as the turing machine.

Note

Also mention DCFL (which is between reg and CFL), CS (which is between CFL and REC)

Definition: A grammar $G = (V,T,S,P)$ is unrestricted if all productions are of the form

$u \rightarrow v$

where $u \in (V \cup T)^+$ and $v \in (V \cup T)^*$ .

No conditions are imposed on the productions. You can have any number of variables and terminals on the left hand side.

Example 1

Let $G = (\{S,A,X\}, \{a,b\},S,P), P =$

$S \rightarrow bAaaX$

$bAa \rightarrow abA$

$AX \rightarrow \lambda$

A derivation of $aab$ is: (the left hand side that is replaced is underlined)

$S \Rightarrow \underline{bAa}aX \Rightarrow a\underline{bAa}X \Rightarrow aab\underline{AX} \Rightarrow aab$

Example 2

Find an unrestricted grammar $G$ such that $L(G) = \{a^nb^nc^n | n> 0\}$

$G = (V,T,S,P)$

$V = \{S,A,B,D,E,X\}$

$T = \{a,b,c\}$

$P =$

$\begin{split}\begin{array}{lll} 1) S \rightarrow AX & \ \ \ \ \ \ & 7) Db \rightarrow bD \\ 2) A \rightarrow aAbc & \ \ \ \ \ \ & 8) DX \rightarrow EXc \\ 3) A \rightarrow aBbc & \ \ \ \ \ \ & 9) BX \rightarrow \lambda \\ 4) Bb \rightarrow bB & \ \ \ \ \ \ & 10) cE \rightarrow Ec \\ 5) Bc \rightarrow D & \ \ \ \ \ \ & 11) bE \rightarrow Eb \\ 6) Dc \rightarrow cD & \ \ \ \ \ \ & 12) aE \rightarrow aB \\ \end{array}\end{split}$

Change the last rule to $DX \rightarrow c$ and you can derive the string $aaabbcbcc$ , moves a $c$ in the wrong place to the end of the string…

To derive string $aaabbbccc$ , use productions 1, 2 and 3 to generate a string that has the correct number of a’s b’s and c’s. The a’s will all be together, but the b’s and c’s will be intertwined.

$S \Rightarrow AX \Rightarrow aAbcX \Rightarrow aaAbcbcX \Rightarrow aaaBbcbcbcX$

Use a $B$ to move right through a group of $B$ ‘s until it sees a $c$ . Replace the $c$ by a $D$ , and use the $D$ to move right to the end of the string. Then write the $c$ at the end of the string. Use an $E$ to move back to the left.

$aaaBbcbcbcX \Rightarrow aaabBcbcbcX \Rightarrow aaabDbcbcX$

$\Rightarrow aaabbDcbcX \Rightarrow aaabbcDbcX \Rightarrow aaabbcbDcX$

$\Rightarrow aaabbcbcDX \Rightarrow aaabbcbcEXc$

$\Rightarrow aaabbcbEcXc$

$\stackrel{*}{\Rightarrow} aaaEbbcbcXc \Rightarrow aaaBbbcbcXc$

Repeat this process until all the $c$ ‘s have been moved to the end of the string. Then remove the $X$ from the string.

$aaaBbbcbcXc \stackrel{*}{\Rightarrow} aaaBbbbXccc \stackrel{*}{\Rightarrow} aaabbbBXccc \Rightarrow aaabbbccc$

Theorem 6

Theorem: If $G$ is an unrestricted grammar, then $L(G)$ is recursively enumerable.

Proof:

List all strings that can be derived in one step.

$S \Rightarrow w$
List all strings that can be derived in two steps.

$S \Rightarrow x \Rightarrow w$
List all strings that can be derived in three steps.
Continue in this way for strings deriveable in any finite number of steps.
Therefore, it is possible to enumerate all strings in the language.

Theorem 7

Theorem: If $L$ is recursively enumerable, then there exists an unrestricted grammar $G$ such that $L = L(G)$ .

Proof: (Sketch!)

L is recursively enumerable.

$\Rightarrow$ there exists a TM $M$ such that $L(M) = L$ .

$M = (Q, \Sigma, \Gamma, \delta, q_0, B, F)$

Idea $M$ starts with $w$ and eventually ends up with a final state.

$q_0w \stackrel{*}{\vdash} x_1q_fx_2$ for some $q_f \in F, x_1, x_2 \in \Gamma^*$

Construct an unrestricted grammar $G$ such that $L(G) = L(M)$ .

But in $G$ , grammar starts with $S$ and eventually derives $w$ , $S \stackrel{*}{\Rightarrow}w$

So the constructed grammar will mimic the Turing machine in reverse.

Three steps:

1. $S \stackrel{*}{\Rightarrow} B \ldots B\#xq_fyB\ldots B$

with $x, y \in \Gamma^*$ for every possible combination

2. $B \ldots B\#xq_fyB\ldots B \stackrel{*}{\Rightarrow} B\ldots B\#q_0wB\ldots B$

by following rules that mimic transitions in reverse order.

3. $B\ldots B\#q_0wB\ldots B \stackrel{*}{\Rightarrow} w$

Here just remove the blanks, and $\# q_0$ .

So here is the constructed grammar.

$G = (V,T,S,P)$

$T = \Sigma$

$V = \{\Gamma - \Sigma\} \cup Q \{\#\} \cup \{S,A\}$

$P$ for each of the three above are:

1. For $S\stackrel{*}{\Rightarrow}B\ldots B\#xq_fyB\ldots B$

$S \rightarrow BS \mid SB \mid \#A$

Replace $S$ with lots of blanks and then finally a #`

$A \rightarrow aA \mid Aa \mid q$

(for every $a \in \Gamma$ and $q \in F$ )

then generate the strings of symbols finishing off with a final state.

2. For $B\ldots B\# xq_fyB\ldots B \stackrel{*}{\Rightarrow} B\ldots B\# q_0wB\ldots B$

Create the rules that mimic what the TM does in reverse order.

Mimic left and right moves.

For each $\delta(q_i,a) = (q_j,b,R)$

Add to $P$ , $bq_j \rightarrow q_ia$

For each $\delta(q_i,a)=(q_j,b,L)$

add to $P$ , $q_jcb \rightarrow cq_ia$ for every

$c \in \Gamma$ .

3. For $B\ldots B\# q_0wB\ldots B \stackrel{*}{\Rightarrow} w$

To get rid of $\# q_0$ and blanks,

$\# q_0 \rightarrow \lambda$

$B \rightarrow \lambda$

Then show that $S \stackrel{*}{\Rightarrow} w$ iff $q_0w \stackrel{*}{\vdash} x_1q_fx_2$ for $q_f \in F$

Definition: A grammar $G$ is context-sensitive if all productions are of the form

$x \rightarrow y$

where $x,y \in (V \cup T)^{+}$ and $|x|\le |y|$

Can be shown that another way to define these is that all productions are of the form:

$xAy \rightarrow xvy$

This is equivalent to saying $A \rightarrow v$ can be applied in the context of $x$ on the left and $x$ on the right.

Definition: $L$ is context-sensitive (CSL) if there exists a context-sensitive grammar $G$ such that $L = L(G)$ or $L = L(G) \cup \{\lambda\}$ .

In the definition of the grammar, we can’t have any lambda rules.

We put $\lambda$ in there so we can claim that CFL $\subset$ CSL

Theorem: For every CSL $L$ not including $\lambda$ , $\exists$ an LBA $M$ such that $L = L(M)$ .

Theorem: If $L$ is accepted by an LBA $M$ , then $\exists$ CSG $G$ such that $L(M) = L(G)$ .

Theorem: Every context-sensitive language $L$ is recursive.

Theorem: There exists a recursive language that is not CSL.

Note

Section 11.3 covers context-sensitive languages (CSL). These languages lie between the context-free languages and the recursive languages. CSL’s and LBA’s (linear bounded automata) represent the same class of languages.

OpenDSA Stand-alone Modules

Chapter 0 modules

287. Recursively Enumerable Languages¶

287.1. Recursively Enumerable Languages¶

287.1.1. Enumeration procedure for recursive languages¶

287.1.2. Enumeration procedure for recursively enumerable languages¶