280. Properties of Context-Free Languages¶

280.1. Properties of Context-Free Languages¶

Note

We will not cover Theorem 8.2

Which of the following languages are CFL?

$L = \{a^nb^nc^j \mid 0 < n\le j\}$

Note

NOT CFL
$L = \{a^nb^ja^nb^j \mid n>0, j>0\}$

Note

NOT CFL
$L = \{a^nb^ja^kb^p \mid n+j \le k+p, n>0, j>0, k>0, p>0 \}$

Note

CFL
$L = \{a^nb^ja^jb^n \mid n>0, j>0\}$

Note

CFL

Pumping Lemma for Regular Languages

Let $L$ be a regular language, then there is a constant $m$ such that $w\in L$ , $|w|\ge m$ , $w = xyz$ such that

$|xy| \le m$

$|y| \ge 1$

for all $i\ge 0, xy^iz \in L$

We were able to show that $a^nb^n$ is not a regular language.

Pumping Lemma for CFL’s

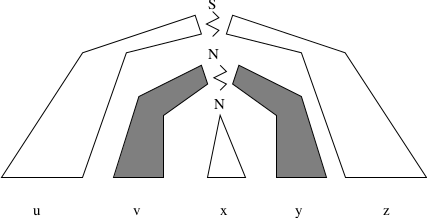
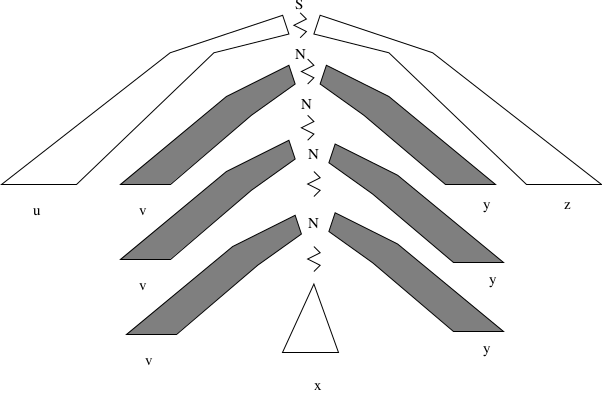
Let $L$ be any infinite CFL. Then there is a constant $m$ depending only on $L$ , such that for every string $w$ in $L$ , with $|w| \ge m$ , we may partition $w = uvxyz$ such that:

$|vxy| \le m$ , (limit on size of substring)

$|vy| \ge 1$ , ( $v$ and $y$ not both empty)

For all $i \ge 0, uv^ixy^iz \in L$

Proof: (sketch)

There is a CFG $G$ such that $L = L(G)$ .

Consider the parse tree of a long string in $L$ .

For any long string, some nonterminal $N$ must appear twice in the path.

N∗⇒vNy and
N∗⇒x.
S∗⇒uNz∗⇒uvNyz∗⇒uvxyz
By repeating the v and y subtrees, get
N∗⇒viNyi∗⇒vixyi.

QED

Example 1

Consider $L = \{a^nb^nc^n: n\ge 1\}$ . Show $L$ is not a CFL.

Proof: (by contradiction)

Assume $L$ is a CFL and apply the pumping lemma.

Let $m$ be the constant in the pumping lemma and consider $w = a^mb^mc^m$ . Note $|w|\ge m$ .

Show there is no division of $w$ into $uvxyz$ such that $|vy|\ge 1$ , $|vxy|\le m$ , and $uv^ixy^iz \in L$ for $i = 0, 1, 2, \ldots$ .

Case 1: Neither $v$ nor $y$ can contain 2 or more distinct symbols. If $v$ contains $a$ ‘s and $b$ ‘s, then $uv^2xy^2z \notin L$ since there will be $b$ ‘s before $a$ ‘s.

Thus, $v$ and $y$ can be only $a$ ‘s, $b$ ‘s, or $c$ ‘s (not mixed).

Case 2: $v = a^{t_1}$ , then $y = a^{t_2}$ or $b^{t_3} (|vxy| \le m)$

If $y = a^{t_2}$ , then $uv^2xy^2z = a^{m+t_1+t_2}b^mc^m \notin L$ since $t_1 + t_2 > 0, n(a) > n(b)$ (number of $a$ ‘s is greater than number of $b$ ‘s)

If $y = b^{t_3}$ , then $uv^2xy^2z = a^{m+t_1}b^{m+t_3}c^m \notin L$ since $t_1 + t_3 > 0$ , either $n(a) > n(c)$ or $n(b) > n(c)$ .

Case 3: $v = b^{t_1}$ , then $y = b^{t_2}$ or $c^{t_3}$ .

If $y = b^{t_2}$ , then $uv^2xy^2z = a^mb^{m+t_1+t_2}c^m \notin L$ since $t_1 + t_2 > 0, n(b) > n(a)$ .

If $y = c^{t_3}$ , then $uv^2xy^2z = a^mb^{m+t_1}c^{m+t_3} \notin L$ since $t_1 + t_3 > 0$ , either $n(b) > n(a)$ or $n(c) > n(a)$ .

Case 4: $v = c^{t_1}$ , then $y = c^{t_2}$ .

Then, $uv^2xy^2z = a^mb^mc^{m+t_1+t_2} \notin L$ since $t_1 + t_2 > 0, n(c) > n(a)$ .

Thus, there is no breakdown of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ and for all $i\ge 0$ , $uv^ixy^iz$ is in $L$ .

This is a contradiction, thus, $L$ is not a CFL. Q.E.D.

Example 2

Why would we want to recognize a language of the type $\{a^nb^nc^n: n\ge 1\}$ ?

Recognize underlined words:

$\underline{word}$ is stored as $word\beta\beta\beta\beta\ \_\ \_\ \_\ \_$ where $\beta$ represents a backspace.

Example 3

Consider $L = \{a^nb^nc^p : p > n > 0 \}$ . Show that $L$ is not a CFL.

Proof:

Assume $L$ is a CFL and apply the pumping lemma. Let $m$ be the constant in the pumping lemma and consider $w = a^mb^mc^{m+1}$ . Note: $|w| \ge m$ .

Show that there is no division of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ , and $uv^ixy^iz \in L$ for $i = 0, 1, 2, \ldots$ .

Case 1: Neither $v$ nor $y$ can contain 2 or more distinct symbols. If $v$ contains a’s and b’s, then $uv^2xy^2z \notin L$ since there will be b’s before a’s.

Thus, $v$ and $y$ can be only a’s, b’s, or c’s (not mixed).

Case 2: $v = a^{t_1}$ , then $y = a^{t_2}$ or $b^{t_3} (|vxy| \le m)$

If $y = a^{t_2}$ , then $uv^2xy^2z = a^{m+t_1+t_2}b^mc^{m+1} \notin L$ since $t_1 + t_2 \ge 1, n(a) > n(b)$ .

If $y = b^{t_3}$ , then $uv^2xy^2z = a^{m+t_1}b^{m+t_3}c^{m+1} \notin L$ since $t_1 + t_3 \ge 1$ , either $n(c)$ is not $> n(a)$ or $n(c)$ is not $> n(b)$ .

Case 3: $v = b^{t_1}$ , then $y = b^{t_2}$ or $c^{t_3}$ .

If $y = b^{t_2}$ , then $uv^2xy^2z = a^mb^{m+t_1+t_2}c^{m+1} \notin L$ since $t_1 + t_2 \ge 1, n(b) > n(a)$ .

If $y = c^{t_3}$ , then $uv^0xy^0z = a^mb^{m-t_1}c^{m+1-t_3} \notin L$ since $t_1 + t_3 \ge 1$ , either $n(b) < n(a)$ or $n(c)$ is not $> n(a)$ .

Case 4: $v = c^{t_1}$ , then $y=c^{t_2}$ .

Then, $uv^0xy^0z = a^mb^mc^{m+1 -t_1-t_2} \notin L$ since $t_1 + t_2 \ge 1, n(c)$ is not $> n(a)$ .

Thus, there is no breakdown of $w$ into $uvxyz$ such that $|vy| \ge 1, |vxy| \le m$ and for all $i\ge 0, uv^ixy^iz$ is in $L$ .

Contradiction, thus, $L$ is not a CFL. Q.E.D.

Example 4

Consider $L = \{a^jb^k: k = j^2\}$ . Show $L$ is not a CFL.

Proof:

Assume $L$ is a CFL and apply the pumping lemma. Let $m$ be the constant in the pumping lemma and consider $w = a^mb^{m^2}$ .

Show there is no division of $w$ into $uvxyz$ such that $|vy| \ge 1, |vxy| \le m$ , and $uv^ixy^iz \in L$ for $i = 0, 1, 2, \ldots$ .

Case 1: Neither $v$ nor $y$ can contain 2 or more distinct symbols. If $v$ contains a’s and b’s, then $uv^2xy^2z \notin L$ since there will be b’s before a’s.

Thus, $v$ and $y$ can be only a’s, and then b’s (not mixed).

Case 2: $v = a^{t_1}$ , then $y = a^{t_2}$ or $b^{t_3}$ .

If $y=a^{t_2}$ , then $uv^2xy^2z = a^{m+t_1+t_2}b^{m^2} \notin L$ since $0 < t_1 + t_2 \le m$ , not enough b’s.

If $y=b^{t_3}$ , then $uv^2xy^2z = a^{m+t_1}b^{m^2+t_3} \notin L$ since $0 < t_1 + t_3 \le m$ , if $t_1 = 0$ , too many b’s. If $t_1 = 1$ , $(m+1)^2 = m^2 +2m+1$ , so for $t_1\ge 1$ , there will be too few b’s.

Case 3: $v=b^{t_1}$ , then $y = b^{t_2}$ .

Then, $uv^2xy^2z = a^mb^{m^2 + t_1 + t_2} \notin L$ since $t_1 + t_2 > 0$ , not enough a’s.

Thus, there is no breakdown of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ and for all $i \ge 0, uv^ixy^iz$ is in $L$ .

Contradiction, thus, $L$ is not a CFL. Q.E.D.

Exercise

Prove the following is not a CFL by applying the pumping lemma. (Answer is at the end of this module).

$L = \{ a^{2n}b^{2m}c^nd^m : n,m \ge 0 \}$ .

Example 5

Consider $L = \{w{\bar w}w : w\in \Sigma^*\}, \Sigma = \{a, b\}$ , where $\bar w$ is the string $w$ with each occurence of $a$ replaced by $b$ and each occurence of $b$ replaced by $a$ . For example, $w = baaa, {\bar w} = abbb, w{\bar w} = baaaabbb$ . Show $L$ is not a CFL.

Proof:: Assume $L$ is a CFL and apply the pumping lemma. Let $m$ be the constant in the pumping lemma and consider $w = a^mb^ma^m$ .

Show there is no division of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ , and $uv^ixy^iz \in L$ for $i = 0, 1, 2, \ldots$ .

(Note: $v$ and $y$ could be mixed a’s and b’s and still be in the language).

(Note: I will use a to represent the a’s in the front of $w$ and $A$ to represent the a’s at the end of $w$ when it is not clear.)

Case 1: $v = a^{t_1}$ , then $y=a^{t_2}, b^{t_3}$ or $a^{t_2}b^{t_3}$ .

If $y=a^{t_2}$ , then $uv^2xy^2z = a^{m+t_1+t_2}b^ma^m \notin L$ since $t_1+t_2 > 0$ , more a’s on left than on right.

If $y=b^{t_3}$ , then $uv^2xy^2z = a^{m+t_1}b^{m+t_3}a^m \notin L$ since $t_1 + t_3 > 0$ , either more a’s on left than on right, or more b’s than a’s on the right.

If $y = a^{t_2}b^{t_3}$ , then $uv^0xy^0z = a^{m-t_1-t_2}b^{m-t_3}a^m \notin L$ since $t_1 + t_2 + t_3 > 0$ , either number of a’s on left and right not equal, or number of b’s not equal to number of a’s on right.

Case 2: $v=a^{t_1}b^{t_2}$ , then $y=b^{t_3}$ . Then $uv^0xy^0z = a^{m -t_1}b^{m-t_2-t_3}a^m \notin L$ since $t_1 + t_2 + t_3 > 0$ , either number of a’s on left and right not equal, or number of b’s not equal to number of a’s on right.

Case 3: $v = b^{t_1}$ , then $y=b^{t_2}, A^{t_3}$ , or $b^{t_2}A^{t_3}$ .

If $y = b^{t_2}$ , then $uv^2xy^2z = a^mb^{m+t_1+t_2}a^m \notin L$ since $t_1+t_2 > 0$ , $n(b) \neq n(a)$ on either side.

If $y=A^{t_3}$ , then $uv^2xy^2z = a^mb^{m+t_1}a^{m+t_3} \notin L$ since $t_1 + t_3 > 0$ , either $n(a)$ on left and right not equal, or $n(b)$ not equal to number of a’s on left.

If $y=b^{t_2}A^{t_3}$ , then $uv^0xy^0z = a^mb^{m-t_1-t_2}a^{m-t_3} \notin L$ since $t_1 + t_2 + t_3 > 0$ , either $n(a)$ on left and right not equal, or $n(b)$ not equal to number of a’s on left.

Case 4: $v = b^{t_1}A^{t_2}$ , then $y = A^{t_3}$ .

Then $uv^0xy^0z = a^mb^{m-t_1}a^{m-t_2-t_3} \notin L$ since $t_1 + t_2 + t_3 > 0$ , either $n(a)$ on left and right not equal, or $n(b)$ not equal to number of a’s on left.

Case 5: $v=A^{t_1}$ , then $y=A^{t_2}$ .

Then $uv^0xy^0z = a^mb^ma^{m-t_1 -t_2} \notin L$ since $t_1+t_2 > 0$ , $n(a)$ on left not equal to $n(a)$ on right.

Thus, there is no breakdown of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ and for all $i \ge 0$ , $uv^ixy^iz$ is in $L$ .

Contradiction, thus, $L$ is not a CFL. Q.E.D.

Example 6

Consider $L = \{a^nb^pb^pa^n\}$ . $L$ is a CFL. The pumping lemma should apply!

Let $m \ge 4$ be the constant in the pumping lemma. Consider $w = a^mb^mb^ma^m$ .

We can break $w$ into $uvxyz$ , with:

$u = a^mb^{m-2} \qquad v = b \qquad x = bb \qquad y = b \qquad z = b^{m-2}a^m$

Thus, $|vy| \ge 1, |vxy| \le m$ , and for all $i \ge 0, uv^ixy^iz = a^mb^{m+i}b^{m+i}a^m \in L$ .

If you apply the pumping lemma to a CFL, then you should find a partition of $w$ that works!

Note

This is not a proof that a language is CFL! Why not?

280.1.1. (Chap 8.2) Closure Properties of CFLs¶

Example: $L=\{a^nb^n | n>0\}$ , $L\circ L = \{a^nb^na^mb^m | n>0, m>0 \}$

Theorem 1

CFL’s are closed under union, concatenation, and star-closure.

Proof:

Given 2 CFG $G_1 = (V_1,T_1,S_1,P_1)$ and $G_2 = (V_2,T_2,S_2,P_2)$

* Union:

Construct $G_3$ such that $L(G_3) = L(G_1) \cup L(G_2)$ .

$G_3 = (V_3,T_3,S_3,P_3)$

$V_3 = V_1 \cup V_2 \cup \{S_3\}, T_3 = T_1 \cup T_2$ , and $P_3 = P_1 \cup P_2 \cup \{S_3 \rightarrow S_1 | S_2 \}$ .

* Concatenation:

Construct $G_3$ such that $L(G_3) = L(G_1) \circ L(G_2)$ .

$G_3 = (V_3,T_3,S_3,P_3)$

$V_3 = V_1 \cup V_2 \cup \{S_3\}, T_3 = T_1 \cup T_2$ , and $P_3 = P_1 \cup P_2 \cup \{S_3 \rightarrow S_1S_2 \}$ .

* Star-Closure

Construct $G_3$ such that $L(G_3) = L(G_1)^*$

$G_3 = (V_3,T_3,S_3,P_3)$

$V_3 = V_1 \cup \{S_3\}, T_3 = T_1$ , and $P_3 = P_1 \cup P_2 \cup \{S_3 \rightarrow S_1S_3|\lambda \}$ .

QED.

Theorem 2

CFL’s are NOT closed under intersection and complementation.

Proof:

* Intersection:

Let $L_1 = \{a^nb^nc^m | n,m > 0\}$ and $L_2 = \{a^nb^mc^m | n,m> 0\}$

$L_1$ and $L_2$ are CFLs

Then $L_1 \cap L_2 = \{a^nb^nc^n | n >0 \}$ is not CFL.

* Complementation:

Set identity:

$L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}}$

Note

Show Venn Diagram!

Thus, CFLs are not closed under complementation.

Note

Example for theorem below:

L1={anbman|m>0,n>0}
L2={w|w∈Σ∗ and w has an even
number of b’s}, Σ={a,b},
L1∪L2={anbmbman} is a CFL.

Theorem 3

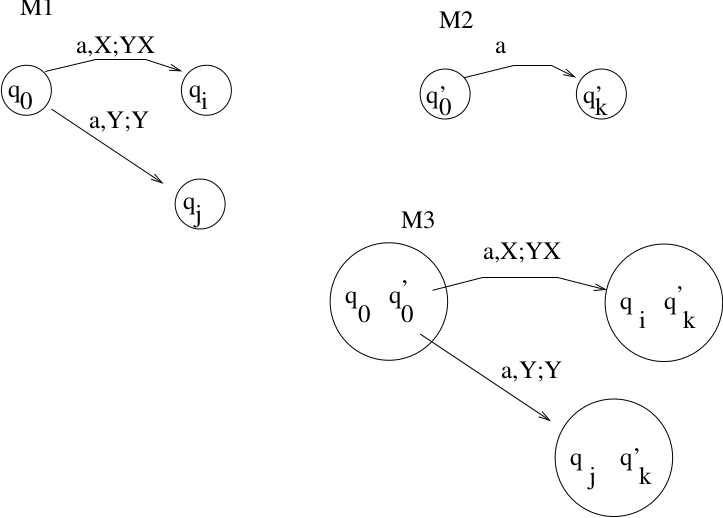
CFL’s are closed under regular intersection. If $L_1$ is CFL and $L_2$ is regular, then $L_1 \cap L_2$ is CFL.

Proof: (sketch)

This proof is similar to the construction proof in which we showed regular languages are closed under intersection. We take a NPDA for $L_1$ and a DFA for $L_2$ and construct a NPDA for $L_1 \cap L_2$ .

$M_1 = (Q_1,\Sigma, \Gamma, {\delta}_1, q_0, z, F_1)$ is an NPDA such that $L(M_1) = L_1$ .

$M_2 = (Q_2,\Sigma, {\delta}_2, q_0^{'}, F_2)$ is a DFA such that $L(M_2) = L_2$ .

Construct NPDA $M_3 = (Q_3,\Sigma, \Gamma, {\delta}_3, (q_0,q_0^{'}), z, F_3)$ where $Q_3 = Q_1 \times Q_2$ , and $F_3 = \{(q,p) | q\in F_1, p\in F_2\}$ .

Example of replacing arcs (NOT a Proof!):

Note this is not a proof, but sketches how we will combine the DFA and NPDA. We must formally define ${\delta}_3$ . If

$(q_k,x) \in {\delta}_1(q_i,a,b)$

$\delta_2(q_j^{'},a) = q_l^{'}$

then

$((q_k,q_l^{'}),x) \in {\delta}_3((q_i,q_j^{'}),a,b)$

Must show

$((q_0,q_0^{'}),w,z) \stackrel{*}{\vdash} ((q_i,q_j^{'}),\lambda,x)$

$(q_i,q_j^{'})\in F_3$

if and only if

$(q_0,w,z) \stackrel{*}{\vdash} (q_i,\lambda,x)$

$(q_0^{'},w) \stackrel{*}{\vdash} (q_j^{'},\lambda)$

$q_i \in F_1$ and $q_j^{'}\in F_2$

Must show:

w in L(M_3)` iff $w \in L(M_1)$ and $w \in L(M_2)$ .

QED.

NOTE: Why doesn’t this proof work for if we try to construct an NPDA that represents the intersection of two NPDA’s? Need 2 stacks.

Questions about CFL:

1. Decide if CFL is empty?

Know how to get rid of useless variables and productions, if there is anything left, then CFL is not empty.

2. Decide if CFL is infinite?

Get rid of useless variables and productions, $\lambda$ -rules, and unit productions. Then if there is a variable that repeats $A \stackrel{*}{\Rightarrow} xAy$ , then $L$ is infinite.

Note

What type of language is a grammar that has this property? How do we recognize it automatically?

Example 7

Consider $L = \{ a^{2n}b^{2m}c^nd^m : n,m \ge 0 \}$ . Show $L$ is not a CFL.

Proof:: Assume $L$ is a CFL and apply the pumping lemma. Let $m$ be the constant in the pumping lemma and consider $w = a^{2m}b^{2m}c^md^m$ .

Show there is no division of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ , and $uv^ixy^iz \in L$ for $i = 0, 1, 2, \ldots$ .

Case 1: Neither $v$ nor $y$ can contain 2 or more distinct symbols. If $v$ contains a’s and b’s, then $uv^2xy^2z \notin L$ since there will be b’s before a’s.

Thus, $v$ and $y$ can be only a’s, b’s, c’s, or d’s (not mixed).

Case 2: $v = a^{t_1}$ , then $y = a^{t_2}$ or $b^{t_3} (|vxy| \le m$)$ .

If $y = a^{t_2}$ , then $uv^2xy^2z = a^{2m+t_1+t_2}b^{2m}c^md^m \notin L$ since $t_1 + t_2 > 0$ , the number of a’s is not twice the number of c’s.

If $y=b^{t_3}$ , then $uv^2xy^2z = a^{2m+t_1}b^{2m+t_3}c^md^m \notin L$ since $t_1 + t_3 > 0$ , either the number of a’s ( $n(a)$ ) is not twice $n(c)$ or $n(b)$ is not twice $n(d)$ .

Case 3: $v = b^{t_1}$ , then $y = b^{t_2}$ or $c^{t_3}$ .

If $y=b^{t_2}$ , then $uv^2xy^2z = a^{2m}b^{2m+t_1+t_2}c^md^m \notin L$ since $t_1 + t_2 > 0, n(b) > 2 * n(d)$ .

If $y = c^{t_3}$ , then $uv^2xy^2z = a^{2m}b^{2m+t_1}c^{m+t_3}d^m \notin L$ since $t_1 + t_3 > 0$ , either $n(b) > 2*n(d)$ or $2*n(c) > n(a)$ .

Case 4: $v = c^{t_1}$ , then $y = c^{t_2}$ or $d^{t_3}$ .

If $y = c^{t_2}$ , then $uv^2xy^2z = a^{2m}b^{2m}c^{m+t_1+t_2}d^m \notin L$ since $t_1 + t_2 > 0, 2 * n(c) > n(a)$ .

If $y = d^{t_3}$ , then $uv^2xy^2z = a^{2m}b^{2m}c^{m+t_1}d^{m+t_3} \notin L$ since $t_1 + t_3 > 0$ , either :math:2*n(c) > n(a)` or $2*n(d) > n(b)$ .

Case 5: $v = d^{t_1}$ , then $y = d^{t_2}$ .

Then $uv^2xy^2z = a^{2m}b^{2m}c^md^{m+t_1+t_2} \notin L$ since $t_1 + t_2 > 0, 2*n(d) > n(c)$ .

Thus, there is no breakdown of $w$ into $uvxyz$ such that $|vy| \ge 1$ , $|vxy| \le m$ and for all $i\ ge 0$ , $uv^ixy^iz$ is in $L$ .

Contradiction, thus, $L$ is not a CFL. Q.E.D.

The following “adversary game” is similar to the one used to help prove that a grammar is not regular.

OpenDSA Stand-alone Modules

Chapter 0 modules

280. Properties of Context-Free Languages¶

280.1. Properties of Context-Free Languages¶

280.1.1. (Chap 8.2) Closure Properties of CFLs¶