7.3.1. PDAs and Context Free Languages¶

In this module, we address the relationship between NPDAs and CFLs. Spoiler alert: NPDAs recognize CFLs.

7.3.2. Convert a CFG to a NPDA¶

Settings

Saving...
Server Error
Resubmit

7.3.3. Convert a NPDA to a CFG¶

Now we want to show that given an NPDA, we can construct a CFG. But first, we will show a result to make the next proof easier.

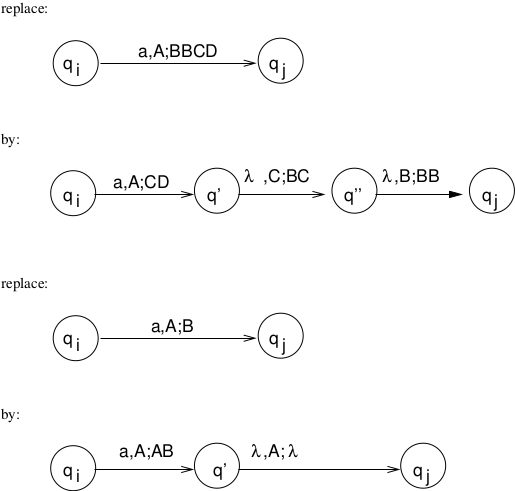
Theorem: Given a NPDA \(M\), there exists a NPDA \(M'\) such that all transitions have the form \(\delta(q_i, a, A) = \{c_1, c_2, \ldots c_n\}\) where

The consequence of this restriction is that each move either increases or decreases the stack contents by a single symbol.

Proof: (sketch)

We can achieve our desired restricted form by replacing any transition in the PDA that has too many or too few variables as follows.

Theorem: If \(L = L(M)\) for some NPDA \(M\), then \(L\) is a CFL.

Want to show that each NPDA represents a CFL, so we will take a NPDA \(M\) and convert it to a CFG. It will be an easier construction if we take the NPDA and put all the transitions in a simpler form.

Proof Sketch:

Given NPDA \(M\), first, construct an equivalent NPDA \(M'\) that meets the simplifying assumptions.

Reverse the process used to generate a PDA from a grammar to simulate the PDA in the grammar

The content of the stack should be reflected in the variable part of the sentential form

The processed input is the terminal prefix of the sentential form