26.1. Balanced Trees¶
The Binary Search Tree has a serious deficiency for practical use as a search structure. That is the fact that it can easily become unbalanced, so that some nodes are deep in the tree. In fact, it is possible for a BST with \(n\) nodes to have a depth of \(n\), making it no faster to search in the worst case than a linked list. If we could keep the tree balanced in some way, then search cost would only be \(\Theta(\log n)\), a huge improvement.
One solution to this problem is to adopt another search tree structure instead of using a BST at all. An example of such an alternative tree structure is the 2-3 Tree or the B-Tree. But another alternative would be to modify the BST access functions in some way to guarantee that the tree performs well. This is an appealing concept, and the concept works well for heaps, whose access functions maintain the heap in the shape of a complete binary tree. Unfortunately, the heap keeps its balanced shape at the cost of weaker restrictions on the relative values of a node and its children, making it a bad search structure. And requiring that the BST always be in the shape of a complete binary tree requires excessive modification to the tree during update, as we see in this example.
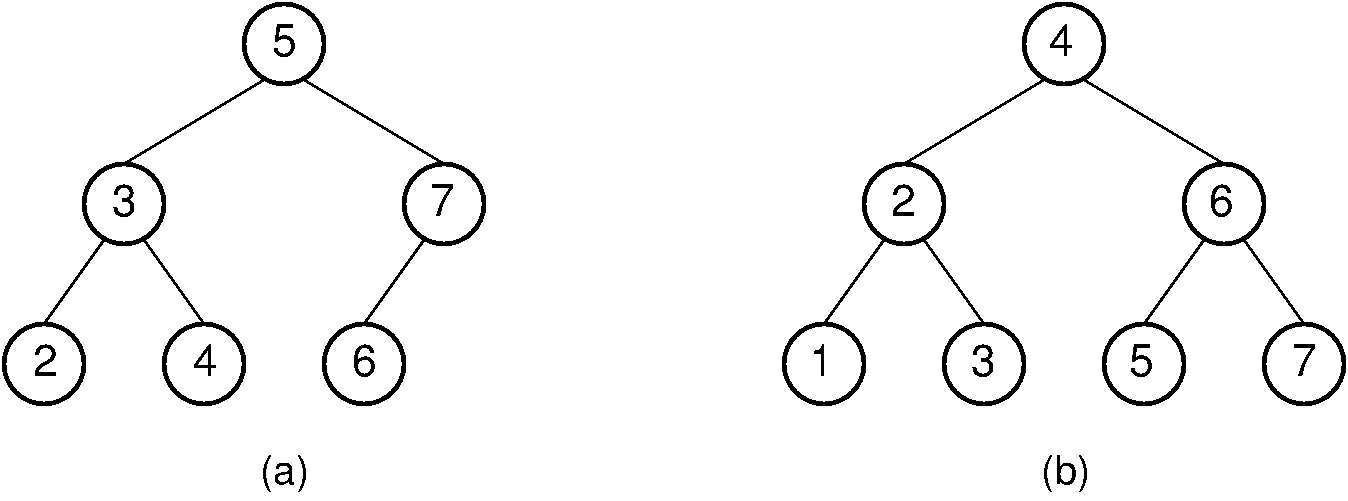
Figure 26.1.1: An attempt to re-balance a BST after insertion can be expensive. (a) A BST with six nodes in the shape of a complete binary tree. (b) A node with value 1 is inserted into the BST of (a). To maintain both the complete binary tree shape and the BST property, a major reorganization of the tree is required.¶
If we are willing to weaken the balance requirements, we can come up with alternative update routines that perform well both in terms of cost for the update and in balance for the resulting tree structure. The AVL tree works in this way, using insertion and deletion routines altered from those of the BST to ensure that, for every node, the depths of the left and right subtrees differ by at most one.
A different approach to improving the performance of the BST is to not require that the tree always be balanced, but rather to expend some effort toward making the BST more balanced every time it is accessed. This is a little like the idea of path compression used by the UNION/FIND algorithm. One example of such a compromise is called the splay tree.
The Red-Black Tree is also a binary tree, but it uses a different balancing mechanism.


