7.1. Pumping Lemma for CFL¶
7.1.1. Which of these is a CFL?¶
Which of the following languages are CFL?\(L = \{a^nb^nc^j \mid 0 < n\le j\}\)\(L = \{a^nb^ja^nb^j \mid n>0, j>0\}\)\(L = \{a^nb^ja^kb^p \mid n+j \le k+p, n>0, j>0, k>0, p>0 \}\)\(L = \{a^nb^ja^jb^n \mid n>0, j>0\}\)
7.1.2. Pumping Lemma: Regular Languages¶
Let \(L\) be an infinite regular language.Then there exists a constant \(m > 0\) such that any \(w \in L\) with \(|w| \ge m\) can be decomposed into three parts as \(w=xyz\) with:\(|xy| \le m\)\(|y| \ge 1\)\(xy^iz \in L\) for all \(i\ge 0\)With this pumping lemma, we were able to show that \(a^nb^n\) is not a regular language.
7.1.3. Pumping Lemma for CFLs: Intuition¶
Suppose a variable repeats, such as: \(A \stackrel{*}{\Rightarrow} vAy\), with \(A \stackrel{*}{\Rightarrow} x\).
The derived string will then contain the substring \(vxy\). There will also be strings in the language that contain substrings \(x, vvxyy, vvvxyyy...\)
A little more complicated because there can be two “pumped” parts (in equal measure of pumped-ness).
Of course, the production is not required to have both $v$ and $y$.
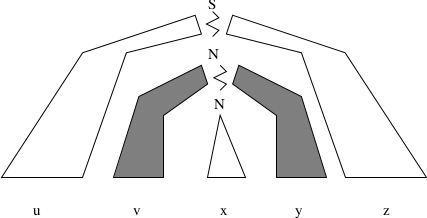
7.1.4. Pumping Lemma for CFLs¶
Let \(L\) be any infinite CFL.Then there exists a constant \(m\) (depending only on \(L\)), such that for every string \(w \in L\), with \(|w| \ge m\), we may partition \(w = uvxyz\) such that:\(|vxy| \le m\), (limit on size of substring)\(|vy| \ge 1\), (\(v\) and \(y\) not both empty)for all \(i \ge 0, uv^ixy^iz \in L\)
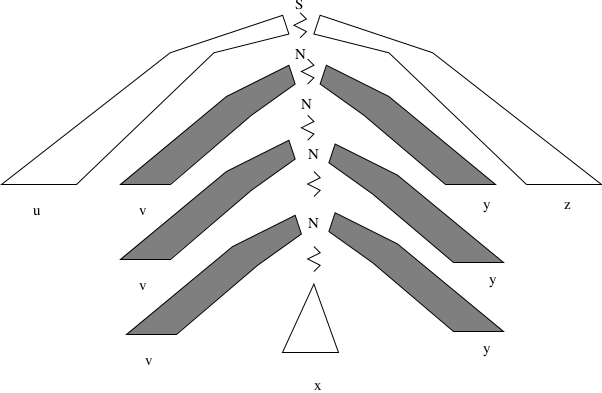
7.1.5. Proof Sketch (1)¶
There is a CFG \(G\) such that \(L = L(G)\).
Consider the parse tree of a long string in \(L\).
For any long string, some nonterminal \(N\) must appear twice in the path.
7.1.6. Proof Sketch (2)¶
\(N \stackrel{*}{\Rightarrow} vNy\) and \(N \stackrel{*}{\Rightarrow} x\).\(S \stackrel{*}{\Rightarrow} uNz \stackrel{*}{\Rightarrow} uvNyz \stackrel{*}{\Rightarrow} uvxyz\)By repeating the \(v\) and \(y\) subtrees, get \(N \stackrel{*}{\Rightarrow} v^iNy^i \stackrel{*}{\Rightarrow} v^ixy^i\).
<< How does this work for grammar \(S \rightarrow aSb | ab\)? >>
7.1.7. Proof Example Problem¶
Consider \(L = \{a^nb^nc^n: n\ge 1\}\).
Why would we want to recognize the language \(\{a^nb^nc^n: n\ge 1\}\)?
Recognize underlined words:
\(\underline{word}\) is stored as \(word\beta\beta\beta\beta\ \_\ \_\ \_\ \_\) where \(\beta\) represents a backspace.
Unfortunately, \(L\) is not a CFL.
7.1.8. Proof (1)¶
Assume \(L\) is a CFL and apply the pumping lemma.Let \(m\) be the constant in the pumping lemma and consider \(w = a^mb^mc^m\). Note \(|w|\ge m\).Show there is no division of \(w\) into \(uvxyz\) such that \(|vy|\ge 1\), \(|vxy|\le m\), and \(uv^ixy^iz \in L\) for \(i = 0, 1, 2, \ldots\).Case 1: Neither \(v\) nor \(y\) may contain 2 or more distinct symbols. If, for example, \(v\) contains a’s and b’s, then \(uv^2xy^2z \notin L\) since there will be b’s before a’s. Likewise for \(y\).Thus, \(v\) and \(y\) each can be only a’s, b’s, or c’s (not mixed).
7.1.9. Proof (2)¶
Case 2: \(v = a^{t_1}\), then \(y = a^{t_2}\) or \(b^{t_3}\) (since \(|vxy| \le m\))If \(y = a^{t_2}\), then \(uv^2xy^2z = a^{m+t_1+t_2}b^mc^m \notin L\) since \(t_1 + t_2 > 0, n(a) > n(b)\) (number of a’s is greater than number of b’s)If \(y = b^{t_3}\), then \(uv^2xy^2z = a^{m+t_1}b^{m+t_3}c^m \notin L\) since \(t_1 + t_3 > 0\), either \(n(a) > n(c)\) or \(n(b) > n(c)\).Case 3: \(v = b^{t_1}\), then \(y = b^{t_2}\) or \(c^{t_3}\).If \(y = b^{t_2}\), then \(uv^2xy^2z = a^mb^{m+t_1+t_2}c^m \notin L\) since \(t_1 + t_2 > 0, n(b) > n(a)\).If \(y = c^{t_3}\), then \(uv^2xy^2z = a^mb^{m+t_1}c^{m+t_3} \notin L\) since \(t_1 + t_3 > 0\), either \(n(b) > n(a)\) or \(n(c) > n(a)\).
7.1.10. Proof (3)¶
Case 4: \(v = c^{t_1}\), then \(y = c^{t_2}\).Then, \(uv^2xy^2z = a^mb^mc^{m+t_1+t_2} \notin L\) since \(t_1 + t_2 > 0, n(c) > n(a)\).Thus, there is no breakdown of \(w\) into \(uvxyz\) such that \(|vy| \ge 1\), \(|vxy| \le m\) and for all \(i\ge 0\), \(uv^ixy^iz\) is in \(L\).This is a contradiction, thus, \(L\) is not a CFL.
7.1.11. Adversary Version (1)¶
Adversary picks some value for \(m\).We pick the string \(w = a^mb^mc^m\).Adversary picks the breakdown for \(w = uvxyz\). Adversary has (bad) choices:\(vxy\) are all a’s, or all b’s, or all c’s.This cannot be pumped.\(vxy\) has either \(v\) or \(y\) a mix of lettersThis cannot be pumped.\(vy\) has between them an equal number of a’s, b’s, and c’s.This is too long.
7.1.12. Adversary Version (2)¶
Note that both \(v\) and \(y\) are pumped the same number of times.If the adversary could pick them with this in mind, then the string might be pumpable.For example, if \(v = a^k\) and \(y = b^kc^k\).But the length restriction kicks in to prevent that(too many b’s between the a’s and c’s in \(w = a^mb^mc^m\)).
7.1.13. (Try to) Prove a CFL not a CFL¶
What if we try to prove that \(L = a^nb^n\) is not context free, by using the pumping lemma?
Pick \(w = a^mb^m\).
Adversary picks \(v = a^k\) and \(y = b^k\). (This is pumpable!)
Of course, this does not prove that \(L\) is context free. Just that we failed to disprove this with the pumping lemma (that is a good thing).
7.1.14. Example¶
Prove that \(L = \left\{ ww \mid w \in \{a, b\}^* \right\}\) is not a CFL.
Consider the string \(w = a^mb^ma^mb^m\).
No matter how the adversary picks \(vxy\), it is not pumpable.
7.1.15. Example¶
Prove that \(L \left\{ a^{n!} \mid n \geq 0 \right\}\) is not a CFL.
We pick \(w = a^{m!}\).Obviously, any decomposition is of the form \(v = a^k\), \(y = a^l\).This is not pumpable.
