6.2.1. Equivalence of NPDA and CFG¶

Now we want to show that NPDA’s and CFG both represent CFL’s.

We will show that we can take any CFG and construct a NPDA, and vice versa.

6.2.2. Any CFG has a NPDA¶

Theorem: For any CFG \(L\) not containing \(\lambda\), \(\exists\) a NPDA \(M\) such that \(L = L(M)\).

Proof (sketch)

Assume (to simplify) that the CFG is in Griebach Normal Form

Grammar \(G' = (V,T,S,P)\) is in GNF if all productions in \(P\) are of the form:

\(A \rightarrow ax\)

\(A \in V, a \in T, x \in V^*\)

We will construct a NPDA that performs a leftmost-derivation of the string.

Given (\(\lambda\) -free) CFL \(L\).

\(\Rightarrow \exists\) CFG \(G\) such that \(L = L(G)\).

\(\Rightarrow \exists\ G'\) in GNF, such that \(L(G) = L(G')\).

6.2.3. Proof Idea¶

At any point in the derivation, we have terminals on the left, and variables on the right.

Terminals on the left are inputs seen.

Variables on the right are kept on the PDA’s stack.

Simply replace the first variable with the derivation that gives us the next input characters, and maybe some variables to stick on the stack.

Big problem: Which production to do next?

No, this is not a problem! Because… non-determinism!!

6.2.4. Proof Example (1)¶

\(S \rightarrow aSbb \mid a\)

Transform to GNF:

\(S \rightarrow aSA \mid a\)

\(A \rightarrow bB\)

\(B \rightarrow b\)

6.2.5. Proof Example (2)¶

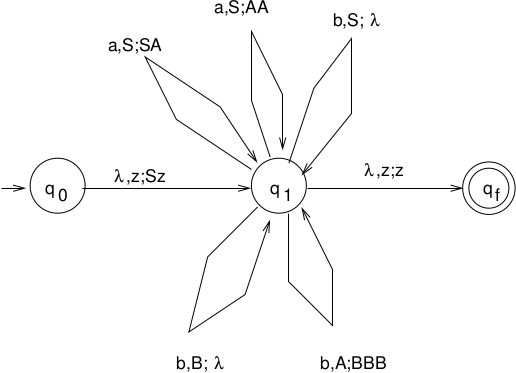
Construct NPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)

\(Q = \{q_0, q_1, q_f\}, \Sigma = T, \Gamma = V \cup \{z\}, F = \{q_f\}\)

1. \(M\) starts by putting \(S\) on the stack

2. For each production

\(A \rightarrow a X_1 X_2 \ldots X_n\)

put \((q_1, X_1 X_2 \ldots X_n)\) in \(\delta(q_1, a, A)\)

(Pop \(A\) from the stack, read “a” from tape, and push \(X_1 X_2 \ldots X_n\) onto the stack)

3. Accept if \(S \stackrel{*}{\Rightarrow} w \in \Sigma^*\) (all variables on the stack are replaced by terminals or \(\lambda\))

6.2.6. Proof Example (3)¶

• \(S \rightarrow aSA \mid a\)

• \(A \rightarrow bB\)

• \(B \rightarrow b\)

6.2.7. Another Example¶

Let \(G' = (V,T,S,P), P =\) | \(S \rightarrow aSA\ |\ aAA\ |\ b\) | \(A \rightarrow bBBB\) | \(B \rightarrow b\)

QUESTION: Is this grammar in GNF?

Trace abbbbb in grammar and pda.

6.2.8. Any NPDA has a CFG (1)¶

Want to show that each NPDA represents a CFG, so we will take a NPDA \(M\) and convert it to a CFG.

It will be an easier construction if we take the NPDA and put all the transitions in a simpler form.

So, there are some side proofs (here and in book) to justify the simplifying assumptions.

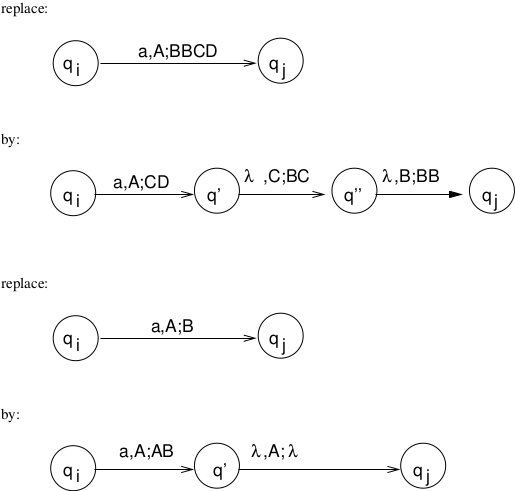
6.2.9. Simplifying Assumptions (1)¶

1. NPDA has a single final state \(q_f\) that is entered if and only if the stack is empty.

2. Can limit the PDA transitions to increase or decrease the stack by one symbol

Theorem: Given a NPDA \(M\), \(\exists\) a NPDA \(M'\) such that all transitions have the form \(\delta(q_i, a, A) = \{c_1, c_2, \ldots c_n\}\) where

\(c_i = (q_j, \lambda)\) or

\(c_i = (q_j, BC)\)

Each move either increases or decreases stack contents by a single symbol.

6.2.10. Simplifying Assumptions (2)¶

6.2.11. Any NPDA has a CFG (2)¶

Theorem: If \(L = L(M)\) for some NPDA \(M\), then \(L\) is a CFG.

Proof Sketch:

Given NPDA \(M\), first, construct an equivalent NPDA \(M'\) that meets the simplifying assumptions.

Reverse the process used to generate a PDA from a grammar to simulate the PDA in the grammar

The content of the stack should be reflected in the variable part of the sentential form

The processed input is the terminal prefix of the sentential form